2. Binomische Formel

Kann man die 2. Binomische Formel so einfach erklären, dass jeder diese versteht? Wir versuchen es hier. Stellt euch vor ein Schüler kommt nach der Schule zu seiner Oma und versucht ihr zu erklären, wie die zweite Binomische Formel funktioniert und wie man sie anwendet. Glaubt ihr eine echte Oma würde die folgenden Erklärungen verstehen?

Schüler: Wir haben heute im Unterricht die 2. Binomische Formel behandelt. Kannst du das noch?

Oma: Ich bin mir nicht sicher was das überhaupt ist.

Schüler: Das ist eine Gleichung aus der Mathematik. Diese sieht so aus:

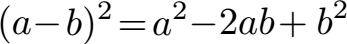
Oma: Sagt mir gar nichts. Was mache ich damit?

Schüler: Dazu muss ich dir glaube ich einmal Beispiele vorrechnen.

Beispiele mit Zahlen

Schüler: Nehmen wir einmal (8 - 4)². Dies ist nichts anderes als eine Abkürzung für (8 - 4)(8 - 4). Die 2. Binomische Formel hilft dabei dies auszurechnen. Die erste Zahl ist unser a, also a = 8. Die zweite Zahl ist unser b, also b = 4.

Oma: Was bedeutet dies für die Binomische Formel?

Schüler: Wir sollen zunächst a² bilden, als 8². Danach sollen wir 2ab finden. Die 2 bleibt stehen, dahinter a mit 8 und b mit 4. Dazwischen jeweils ein Malzeichen. Im Anschluss noch b², also 4². Im Anschluss müssen wir einfach nur noch ausrechnen.

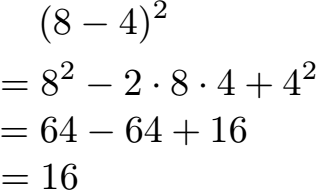
Oma: Was soll das? Ich kann doch einfach (8 - 4) ausrechnen, also 4 und dann quadrieren um auf 16 zu kommen. Da muss ich doch nicht so bescheuert rumrechnen?

Schüler: Das war ja nur eine ganz einfache Einführung um die die 2. Binomische Formel mit Zahlen zu zeigen.

Oma: Und wofür braucht man diese Binomischen Gleichungen überhaupt?

Schüler: Die braucht man zum Beispiel dafür:

• Ausrechnen von Klammern zum Quadrat.
• Das Ausmultiplizieren rückgängig machen.
• Umformen von Gleichungen und Ungleichungen.

Anzeigen:

2. Binomische Gleichung mit Variablen

Schüler: Du brauchst denke ich ein richtiges Beispiel, mit welchem man eine schwierigere Klammer auflösen kann.

Oma: Wird auch Zeit.

Schüler; Die 2. Binomische Formel dient dazu Klammern aufzulösen bei denen Variablen vorkommen. Die Variablen (Buchstaben) stehen für Zahlen, die man noch nicht kennt. Ich rechne mal ein Beispiel vor, bitte nicht gleich erschrecken.

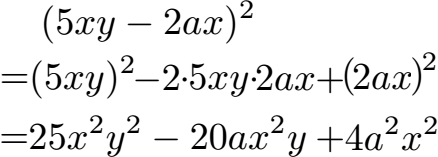
Oma: Das kapiere ich nicht.

Schüler: Das vorne mit 5xy ist unser a, das hinten mit 2ax ist unser b. Wir brauchen für die Lösung a² und b², daher nehmen wir diese beiden Teile und quadrieren sie jeweils. Da wir den ganzen Ausdruck quadrieren müssen setzen wir eine Klammer darum. Dazwischen fehlt uns noch 2ab, also nehmen wir die 2 und multiplizieren die mit a (also 5xy) und multiplizieren dies mit b (also 2ax).

Oma: Ich verstehe nicht wie man das ausrechnet. Also das (5xy)² auf 25x²y² bringen.

Schüler: Wir müssen (5xy)(5xy) ausrechnen. Das erhalten wir mit 5 · 5 = 25, mit x · x = x² und y · y = y².

Oma: Ah OK, jetzt verstehe ich es.

Zweite Binomische Formel Herleitung

Oma: Wie kommt man auf so etwas wie die Binomische Formel oder zweite Binomische Formel?

Schüler: Das nennt man Herleitung. Ich suche diese gerade mal raus. Die Herleitung sieht so aus:

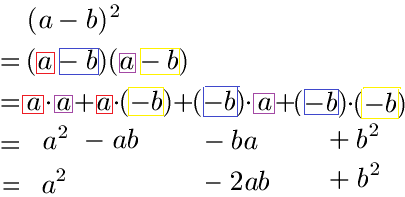
Oma: Wie kommt man selbst darauf?

Schüler: Das ist wie beim Klammern auflösen. Jedes Element der einen Klammer wird mit jedem Element der anderen Klammer multipliziert.

Oma: Brauche ich das noch einmal im Leben?

Schüler: Naja, ist halt "nice to know". Es ist wichtiger Übungen zu den Binomischen Formeln selbst rechnen zu können.

Aufgaben / Übungen Binomische Formeln mit Lösung

Aufgabe 1: Glaubt ihr das Thema Binomische Formeln verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Mit den Übungsaufgaben könnt ihr alle drei Binomischen Formeln geübt werden. Aufgaben können per Klick übersprungen werden. Wie lautet die Lösung dieser Aufgabe?

• (4y + 3z)² = ____

• 16y² + 24yz + 5z²
• 16y² + 24yz + 9z²
• 8y² + 24yz + 9z²
• 16y² + 12yz + 9z²

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.