Umfang Rechteck mit Formeln berechnen

Was ist der Umfang von einem Rechteck? Welche Formeln werden benutzt um den Umfang zu berechnen? Worauf muss ich achten? Ich versuche die Inhalte so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde. Die Inhalte liegen als Text und als Video vor.

Ein Rechteck besteht aus 4 Seiten. Die gegenüberliegenden Seiten sind gleich lang und werden in der Mathematik mit gleichen Variablen (Buchstaben) bezeichnet. Der Umfang eines Rechtecks bedeutet die Länge der 4 Seiten zusammen zu rechnen.

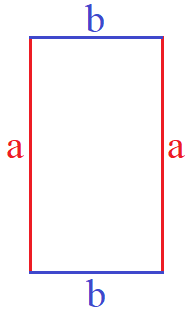
Du kannst dir die Länge der 4 Seiten eines Rechtecks sehr gut mit dem folgenden Tisch verdeutlichen. Der Umfang ist nichts anderes als ein Mal um den ganzen Tisch direkt an der Kante zu laufen. Und zwar ganz präzise an der Kante.

Der Umfang eines Rechtecks ist damit U = a + b + a + b. In der Mathematik werden Gleichungen und Formeln verwendet um Berechnungen durchzuführen. Diese Formeln sehen wir uns nun mit Beispielen an.

Formel und Beispiel zum Rechteck Umfang

Der Umfang eines Rechtecks sagt aus, dass die beiden unterschiedlichen Seitenlängen eines Rechtecks verdoppelt und addiert werden. In der Formel zum Rechteck ist "U" der Umfang des Rechtecks und "a" und "b" sind die Seitenlängen.

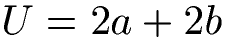
Beispiel Rechteck Umfang:

Als einfaches Beispiel soll die Seitenlänge a = 3 m und die Seitenlänge b = 2 m dienen. Der Umfang des Rechtecks soll berechnet werden. Zum besseren Verständnis kann das Rechteck gezeichnet werden oder zumindest eine grobe Skizze angelegt werden.

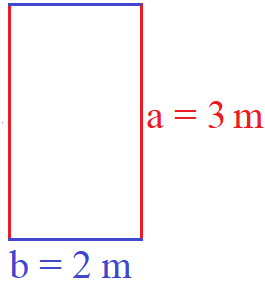
Um den Umfang zu berechnen, verwenden wir die Formel und setzen in diese a = 3 m und b = 2 m ein. Bei der Berechnung der Aufgabe achten wir auf die Regel Punkt vor Strich. Wir rechnen daher zunächst die Multiplikationen aus und erst im Anschluss die Addition.

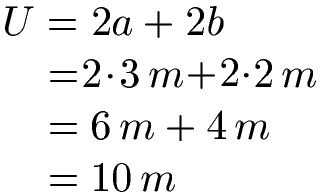
Beim Rechnen mit Längen muss jeweils die Einheit mit berücksichtigt werden. In diesem Fall sind es Längeneinheiten, genauer gesagt Angaben in Metern. Setze daher nicht "3", sondern "3 m" in die Formel ein.

Mit dem Umfang eines Rechtecks lässt sich die Seitenlänge des Rechtecks berechnen. Genauer gesagt lässt sich eine Seitenlänge berechnen, wenn die andere Seitenlänge und der Umfang bekannt ist. Die Formeln zur Seitenlänge lauten:

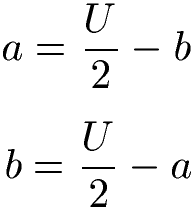
Im nächsten Abschnitt sehen wir uns noch an, wie der Umfang eines Rechtecks mit der Fläche berechnet werden kann. Auch die Längeneinheiten und deren Umrechnung sehen wir uns noch an.

Anzeigen:

Mit Fläche den Umfang berechnen

Der Umfang eines Rechtecks lässt sich mit der Fläche des Rechtecks und der Länge einer Seite berechnen. Zur Erinnerung: Die Fläche "A" gibt an, wie groß das Rechteck ist.

Es gib zwei Formeln um den Umfang des Rechtecks mit der Fläche zu berechnen. In den Formeln steht "U" für den Umfang des Rechtecks, "A" für die Fläche und "a" und "b" sind die Seitenlängen. Verwechsle daher nicht "A" und "a" bei der Berechnung.

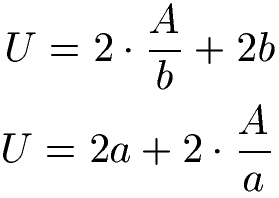
Beispiel Umfang Rechteck mit Fläche:

Ein Rechteck hat eine Fläche von 8 Quadratmeter und die Seite a ist 4 Meter lang. Wie groß ist der Umfang des Rechtecks? Lösung: Dem Text entnehmen wir A = 8 m² und a = 4 m. Da wir "a" kennen, aber "b" nicht, verwenden wir die Formel zum Umfang mit "a" und setzen ein. Von der Reihenfolge der Berechnung zunächst die Multiplikationen berechnen und danach die Addition.

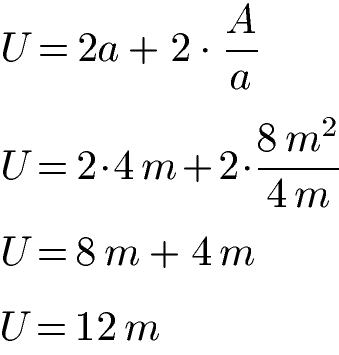
Der Umfang des Rechtecks beträgt 12 Meter.

Einheiten und Längeneinheiten

Der Umfang eines Rechtecks wird mit einer Längeneinheit angegeben. Typische Längeneinheiten sind zum Beispiel Zentimeter und Meter. Die nächste Tabelle zeigt eine Übersicht über wichtige Einheiten und deren Abkürzung.

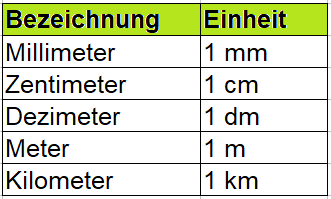
In die Formel zum Umfang eines Rechtecks müssen gleiche Einheiten eingesetzt werden. So darf nicht die eine Seite in Zentimeter und die andere Seite in Metern eingesetzt werden. Daher muss auf gleiche Längeneinheiten umgerechnet werden. Die nächste Grafik zeigt wie zwischen den verschiedenen Einheiten umgerechnet werden kann.

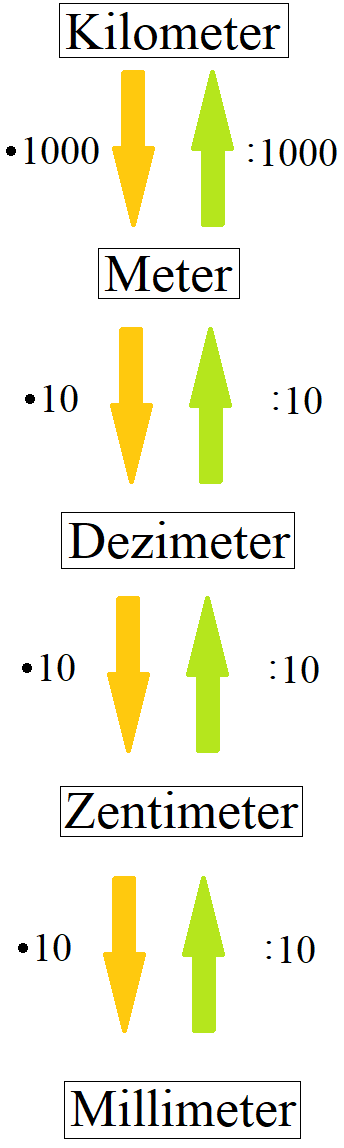
Mehr zur Umrechnung und Beispiele findest du unter Maßeinheiten umrechnen.