Polynomdivision einfach erklärt

Kann man die Polynomdivision so einfach erklären, dass jeder diese versteht? Wir versuchen es hier. Stellt euch vor ein Schüler kommt nach der Schule zu seiner Oma und versucht ihr zu erklären, was diese Polynomdivision ist und wie man sie durchführt. Glaubt ihr eine echte Oma würde die folgenden Erklärungen verstehen?

Schüler: Wir haben heute die Polynomdivision in der Schule behandelt. Weiß du noch was das ist?

Oma: Überhaupt nicht. Wofür braucht man das?

Schüler: In der Schule benutzt man dies um Nullstellen zu berechnen. Ich hatte dir ja mal gezeigt wie man eine Funktion zeichnet. Die Nullstellen sind die Stellen, an denen die Kurve die x-Achse berührt.

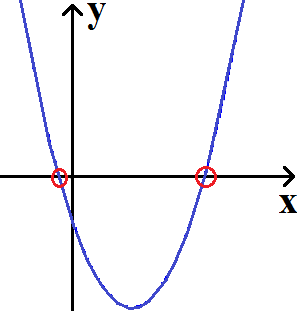
Wofür eine Polynomdivision?

Oma: Na toll. Da rechne ich irgendwelche Schnittpunkt aus. Braucht man so etwas im echten Leben? Anderes gefragt: Wofür braucht man die Polynomdivision noch?

Schüler: Das braucht man schon in der Realität. Wenn in einem Computer Informationen übertragen werden oder Daten von einem Computer zu einem anderen Computer übertragen werden, muss man sicherstellen, dass alles richtig übermittelt wurde. Dafür braucht man die Polynomdivision. Das nennt man dort zyklische Redundanzprüfung (CRC).

Oma: Klingt kompliziert.

Anzeigen:

Polynomdivision Beispiel

Oma: Wie funktioniert eine Polynomdivision?

Schüler: Mit der Polynomdivision berechnet man einen Bruch. Das war bei der Bruchrechnung zum Beispiel 2 : 4 = 0,5. Bei der Polynomdivision kommt jedoch x im Zähler und im Nenner vor. Zum Beispiel x³ - x² - 4x + 4 geteilt durch x - 2. Dieses teilen soll man durchführen.

Oma: Das musst du mir Stück für Stück einmal zeigen.

Schüler: Ich schreibe erst einmal die Aufgabe zum Lösen auf. Das wäre diese hier:

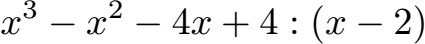
Oma: Wie lege ich los?

Schüler: Wir fangen vorne an mit x³. Diese teilen wir durch das x in der Klammer. Dabei kürzt sich ein x raus: x³ : x = x².

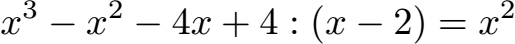
Schüler: Im Anschluss müssen wir in die andere Richtung rechnen. Wir nehmen die x² - welche wir eben berechnet haben - und multiplizieren diese mit der Klammer (x-2). Multiplizieren wir x² mit x erhalten wir wieder x³. Im Anschluss x² mal -2 ergibt -2x².

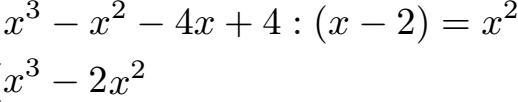
Oma: Ist das x² hinter dem istgleich ein Teil der Lösung?

Schüler: Ja. Die Potenz ist um 1 gesunken, von x³ auf x².

Schritt für Schritt Polynomdivision

Schüler: Machen wir mal weiter: Wir müssen nun eine Subtraktion durchführen. Dazu subtrahieren wir von den x³ - x² am Anfang das was wir eben berechnet haben, also die x³ - 2x².

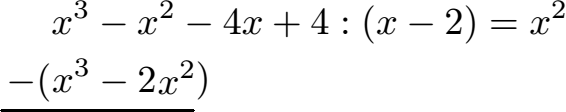
Schüler: Nun führen wir die Subtraktion durch. Vorne haben wir x³ - x³ = 0. Das fällt somit raus. Dahinter -x² - (-2x²) = x². Hier muss man sehr auf die Vorzeichen achten. Im Prinzip rechnet man hier -x² + 2x² = x².

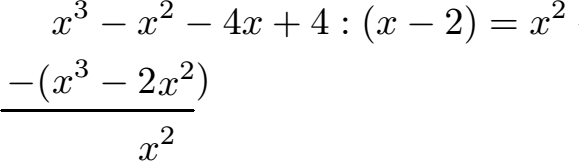
Oma: Es bleibt x² hier übrig. OK und jetzt?

Schüler: Wir ziehen von oben die -4x runter.

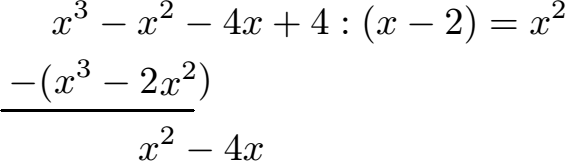
Vorzeichen beachten

Schüler: Jetzt geht es im Prinzip wieder von vorne los. Wir nehmen von den x²- 4x nur die x² und teilen diese durch x. Wir erhalten x² : x = x. Dieses berechnete x schreiben wir hinter das x² im Ergebnis.

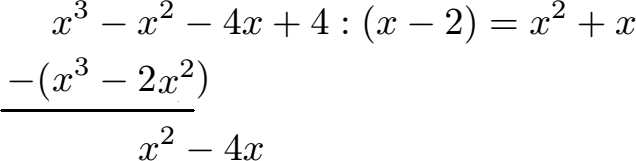
Oma: Jetzt wieder in die andere Richtung rechnen?

Schüler: Ja. Wir multiplizieren das neue x aus dem Ergebnis mit (x - 2). Aus x · x wird x². Aus x · -2 wird -2x. Dies setzen wir wieder in Klammern, welche wir vollständig von dem was darüber steht abziehen müssen.

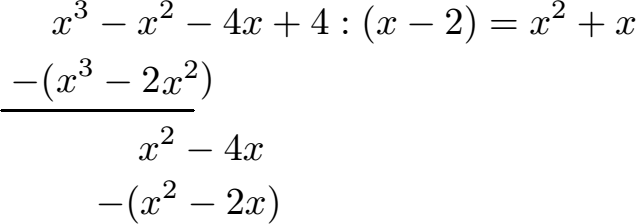
Oma: Lass mich mal versuchen. Wir subtrahieren wieder wie vorne. Das x² vorne fliegt durch die Subtraktion raus. Aus -4x - (-2x) wird -4x + 2x = -2x. Fast vergessen: Die +4 von oben ziehen wir runter.

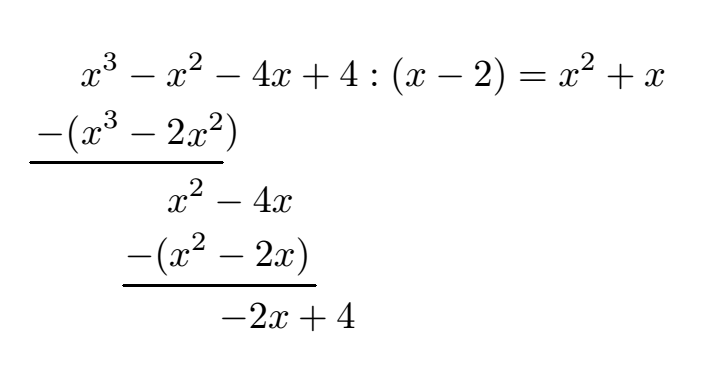
Quadratisches Ergebnis berechnen

Schüler: Stimmt. Wir nehmen wieder den vorderen Term -2x und teilen durch x. Dadurch erhalten wir -2 für unser Ergebnis.

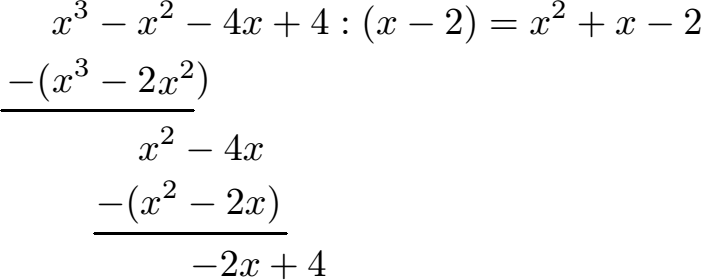
Schüler: Ein letztes zurück multiplizieren. Die -2 aus dem Ergebnis mit (x - 2) liefert -2x + 4. Diese setzen wir ebenfalls wieder in Klammern und schreiben ein Minus davor. Führen wir die Subtraktion aus bleibt 0 übrig. Wir sind fertig mit der Berechnung.

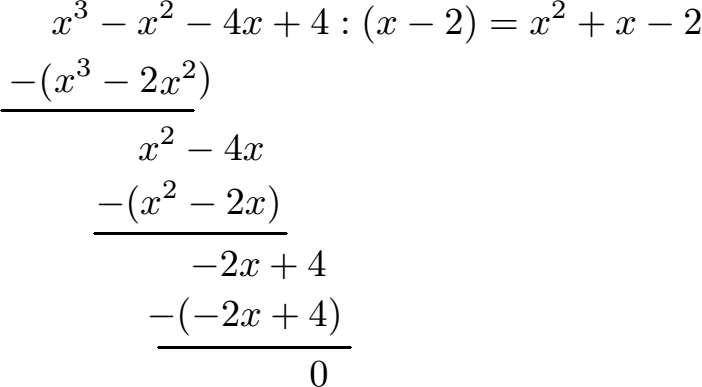
Oma: Das Ergebnis der Polynomdivision ist damit x² + x - 2?

Schüler: Richtig.

Weitere Nullstellen berechnen

Oma: Aber du hattest doch gesagt wir Erfahren die Nullstellen. Das x² + x - 2 ist doch keine Nullstelle?

Schüler: Stimmt. Wir müssten dies auch wieder gleich 0 setzen. Ich meine damit x² + x - 2 = 0. Dies können wir mit der PQ-Formel lösen. Das wird jetzt hier allerdings zu lange werden. Macht man dies erhält man weitere Nullstellen bei x = -2 und x = +1.

Oma: Du sagst weitere Nullstellen. Welche denn noch?

Schüler: Es gibt noch eine dritte Nullstelle. Bei unserer Polynomdivision hatten wir durch (x - 2) geteilt. Aus den (x - 2) können wir direkt ablesen, dass bei x = 2 ebenfalls noch eine Nullstelle ist.

Oma: Gibt es sonst noch etwas, das ich wissen müsste?

Schüler: Manchmal entsteht bei der Polynomdivision ein Rest. Weißt du was das heißt?

Oma: Das ich mich verrechnet habe?

Schüler: Das wäre eine Möglichkeit. Dann sollte man noch einmal nachrechnen. Die andere Möglichkeit ist, dass wir gar nicht durch eine Nullstelle geteilt haben.

Oma: Das ist alles gar nicht so einfach. Wie lerne ich das Thema?

Schüler: In dem du Aufgaben / Übungen dazu selbst rechnest.

Aufgaben / Übungen Polynomdivision

Aufgabe 1:

Glaubt ihr das Thema Polynomdivision verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Da viele Schüler jedoch schon bei Basiswissen scheitern, fangen wir mit einfachen Fragen dazu an. Fragen und Aufgaben können per Klick übersprungen werden.

• Was berechnet man mit der Polynomdivision überhaupt?

• Nullstellen berechnen
• Hypotenuse berechnen
• Produkt berechnen
• Nenner berechnen

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.