Rationale Zahlen ▷ Ist eine Zahl rational?
Geschrieben von: Dennis RudolphMittwoch, 13. April 2022 um 11:35 Uhr
Welche Zahlen sind rational? Welche Arten von Zahlen gehören zu den rationalen Zahlen? Sind Dezimalzahlen rational oder irrational? Die Antworten auf diese Fragen und mehr bekommst du hier. Ich versuche die Inhalte so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde. Die Inhalte liegen als Text und als Video vor.
Einfach erklärt sind rationale Zahlen Brüche bei denen Zähler und Nenner ganze Zahlen sind. Diese Brüche können ausgerechnet werden. Die dabei entstehenden Dezimalzahlen (Kommazahlen) sind ebenfalls rationale Zahlen.
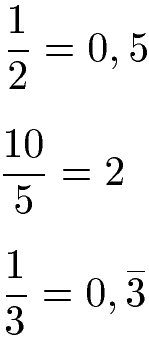
Eine rationale Zahl kann als Bruch oder als Dezimalzahl (Kommazahl) dargestellt werden.
Welche Zahlen sind rational?
Rational sind alle Zahlen die in Form eines Bruchs aus ganzen Zahlen dargestellt werden können. Wird der Bruch ausgerechnet entsteht ebenfalls eine rationale Zahl.
Was gehört alles zu den rationalen Zahlen?
Diese Zahlen gehören zu den rationalen Zahlen: Natürlichen Zahlen, ganze Zahlen, endliche Dezimalzahlen und unendliche Dezimalzahlen mit Perioden.
Natürliche Zahlen:
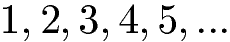
Ganze Zahlen:
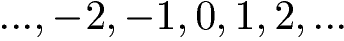
Brüche aus ganzen Zahlen:
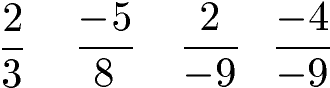
Endliche Dezimalzahlen:
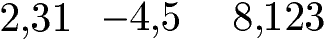
Unendliche Dezimalzahlen mit Perioden:
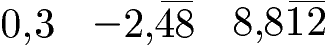
Anzeigen:
Welche Zahlen sind nicht rational?
Zahlen sind nicht rational wenn sie unendlich viele Stellen nach dem Komma aufweisen, die nicht periodisch sind. Beispiele sind die Wurzel aus 5 oder die Wurzel aus minus 3, die Kreiszahl Pi und die eulersche Zahl e.
Werden diese Zahlen berechnet, entstehen unendlich viele Stellen nach dem Komma, die sich jedoch nicht wiederholen. Die folgenden Zahlen sind daher nicht rational.
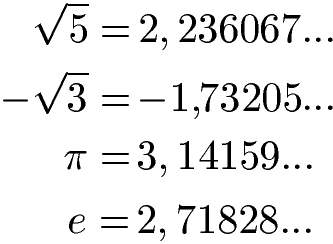
Sind rationale Zahlen unendlich?
Ein Teil der rationalen Zahlen hat unendlich viele Stellen nach dem Komma. Dabei handelt es sich um Brüche oder Dezimalzahlen mit periodischen Ziffern nach dem Komma.
Periodische Ziffern nach dem Komma bedeutet, dass sich alle oder zumindest ein Teil der Stellen nach dem Komma immer wieder wiederholen. Solche Zahlen sind rational, obwohl sie unendlich viele Stellen nach dem Komma aufweisen.
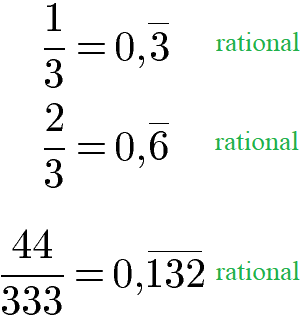
Im Vergleich dazu gibt es Dezimalzahlen mit unendlich vielen Stellen nach dem Komma, die jedoch keine rationalen Zahlen sind.
Die nächste Grafik zeigt vier Wurzel-Beispiele. Werden diese Wurzeln berechnet, entstehen Kommazahlen mit unendlich vielen Stellen nach dem Komma, die sich jedoch nicht wiederholen. Daher sind die Wurzeln aus diesen Beispielen nicht rational.

Sind Wurzeln rationale Zahlen?
Wurzeln sind in manchen Fällen rationale Zahlen, in anderen Fällen sind sie nicht rational. Um dies herauszufinden, muss die Wurzel berechnet werden. Entsteht dabei eine Dezimalzahl mit unendlich vielen Stellen hinter dem Komma (wobei sich diese Stellen nicht wiederholen) handelt es sich um eine irrationale Zahl (= nicht rational). Ansonsten handelt es sich um eine rationale Zahl.

Ist eine Dezimalzahl eine rationale Zahl?
Manche Dezimalzahlen (Kommazahlen) sind rationale Zahlen, andere nicht. Bei der Dezimalzahl handelt es sich um eine rationale Zahl, wenn die Anzahl der Stellen nach dem Komma begrenzt ist.
Die Dezimalzahl ist auch rational, wenn nach dem Komma alle oder ein Teil der Stellen periodisch ist (zu erkennen am Strich über einer oder mehreren Ziffern). Die nächste Grafik zeigt rationale und nicht rationale Dezimalzahlen.

Sind Zahlen oder Brüche rational?
In diesem Abschnitt sehen wir uns einige Zahlen und Brüche (= Divisionen) an und klären, ob diese rational sind oder nicht.
- Ist 6 eine rationale Zahl? Ja, eine natürliche Zahl ist rational.
- Ist 4:5 eine rationale Zahl? Ja, es handelt sich um einen Bruch mit nur ganzen Zahlen.
- Ist 1:3 eine rationale Zahl? Ja, es handelt sich um einen Bruch mit nur ganzen Zahlen.
- Ist 3:4 rational? Ja, es handelt sich um einen Bruch mit nur ganzen Zahlen.
- Ist 4 rational? Ja, ganze und natürliche Zahlen sind rational.
- Ist 3 eine rationale Zahl? Ja, ganze und natürliche Zahlen sind rational.
Gilt das Kommutativgesetz auch für rationale Zahlen?
Die Rechengesetze Kommutativgesetz, Assoziativgesetz und Distrubutivgesetz gelten auch für rationale Zahlen. Diese Rechengesetze sind gültig, egal ob es sich um Dezimalzahlen (Kommazahlen) oder Brüche handelt. Sehen wir uns für das Kommutativgesetz einige Beispiele an
Kommutativgesetz Addition Dezimalzahlen:
Die Reihenfolge der Addition von Dezimalzahlen spielt keine Rolle für das Ergebnis. Die Berechnung erfolgt mit der schriftlichen Addition mit Komma, wobei Komma unter Komma steht. Weitere Beispiele unter schriftliche Addition mit Komma.
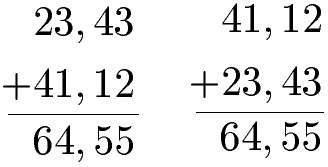
Kommutativgesetz Addition Brüche:
Die Reihenfolge der Addition von Brüchen spielt keine Rolle für das Ergebnis (Summe). Die Berechnung erfolgt mit den Regeln der Bruchrechnung. Es folgt gleich ein einfaches Beispiel. Weitere Beispiele findest du unter Brüche addieren.
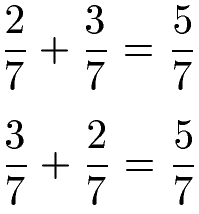
Kommutativgesetz Multiplikation Dezimalzahlen:
Die Reihenfolge der Multiplikation von Dezimalzahlen spielt keine Rolle für das Ergebnis. Die Berechnung erfolgt mit der schriftlichen Multiplikation mit Komma. Weitere Beispiele unter schriftliche Multiplikation mit Komma.
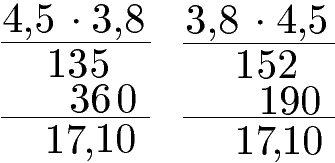
Kommutativgesetz Multiplikation Brüche:
Die Reihenfolge der Multiplikation von Brüchen spielt keine Rolle für das Ergebnis (Produkt). Die Berechnung erfolgt mit den Regeln der Bruchrechnung. Es folgt gleich ein einfaches Beispiel. Weitere Beispiele findest du unter Brüche multiplizieren.
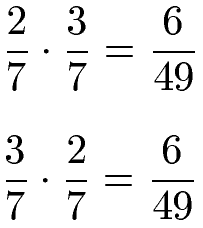
Meistgelesene Inhalte
- Allgemenbildung Quiz
- Prozentrechnung
- Bruchrechnen
- Satz des Pythagoras
- PQ-Formel
- Mitternachtsformel
- Polynomdivision
- Zinsrechnung
- Gleichungen umformen
- Nullstellen bestimmen
- Dreisatz
Neue Artikel
- Rationale Zahlen ▷ Ist eine Zahl rational?
- Bruch in Kommazahl (Dezimalzahl) umwandeln
- Koordinatensystem: Erklärung und Punkte
- Brüche kürzen und erweitern
- Brüche multiplizieren und dividieren
- Rechteck Eigenschaften: Flächeninhalt, Umfang und mehr
- Brüche addieren und subtrahieren
- Sachaufgaben Klasse 5 Mathematik
- Flächeninhalt Rechteck ▯ Beispiele + Erklärung
- Umfang Rechteck mit Formeln berechnen
