PQ-Formel anwenden

Kann man die PQ-Formel so einfach erklären, dass jeder diese versteht? Wir versuchen es hier. Stellt euch vor ein Schüler kommt nach der Schule zu seiner Oma und versucht ihr zu erklären, was die PQ-Formel ist und wie man diese benutzt. Glaubt ihr eine echte Oma würde die folgenden Erklärungen verstehen?

Schüler: Hast du schon einmal etwas von der PQ-Formel gehört?

Oma: Nein.

Schüler: Diese benutzt man um quadratische Gleichungen oder quadratische Funktionen zu lösen.

Oma: Ich verstehe kein Wort. Das musst du mir erklären.

Schüler: Erinnerst du dich noch an das Gleichungen umformen? Dort hatten wir zum Beispiel dies hier:

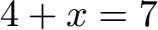
Schüler: Das x war hier 3. Das war ganz einfach zu berechnen. Aber was mache ich wenn ich kein x habe, sondern x · x, also zum Beispiel 3 · 3 oder 4 · 4? Kurz geschrieben wird aus x · x = x². Wenn dies in einer Gleichung vorkommt, wie kann ich dann das x berechnen?

Oma: Da du mich nach der PQ-Formel gefragt hast wirst du sicherlich diese jetzt benutzen.

Schüler: So ist es. Bei einer quadratischen Gleichung (der Lehrer sagt eigentlich gemischt-quadratische Gleichung, aber das ist jetzt mal egal) verwenden wir die PQ-Formel um x zu berechnen. Dies hier ist eine quadratische Gleichung:

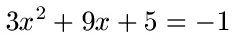
Schüler. Ganz wichtig ist, dass es kein x³, x⁴ oder höher gibt.

PQ-Formel Beispiel

Schüler: Nehmen wir die Gleichung von weiter oben noch einmal:

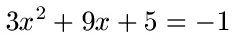
Oma: Was mache ich damit jetzt?

Schüler: Wir haben auf der rechten Seite der Gleichung eine -1 stehen. Hier muss jedoch eine 0 stehen um die Formel anwenden zu können. Daher bringen wir die -1 auf die andere Seite. Wir rechnen auf beiden Seite der Gleichung +1. Dadurch wird aus der 5 eine 6 auf der linken Seite der Gleichung und auf der rechten Seite erhalten wir eine Null.

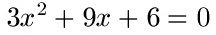
Oma: Das war noch einfach. Was kommt als nächstes?

Schüler: Vor x² steht eine 3. Diese muss weg, wir benötigen nur x². Daher teilen wir die gesamte Gleichung durch 3. Die 3, die 9 und die 6 teilen wir durch 3 und erhalten damit diese Gleichung:

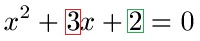
Oma: Wie haben jetzt an der quadratischen Gleichung Umformungen durchgeführt. So nanntest du es zumindest als wir einfache Gleichungen nach x aufgelöst hatten.

Schüler: Richtig. Diese Gleichung hat jetzt die Form um die PQ-Formel anwenden zu dürfen.

Oma: OK. Aber ich weiß immer noch nicht was die PQ-Formel eigentlich ist?

Schüler: Ja, ich wollte dir erst einmal zeigen was eine quadratische Gleichung ist und wie man diese richtig umformt.

Anzeigen:

Die Lösungsformel anwenden

Schüler: Dann machen wir dies doch gerade einmal. Dies hier ist die eigentliche PQ-Formel. Man nennt diese Darstellung auch Lösungsformel.

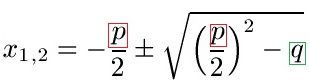
Oma: Ich verstehe nichts. Was soll das?

Schüler: Wir müssen aus der quadratischen Gleichung, die wir eben umgeformt haben, p ablesen und q ablesen.

Oma: Was ist p? Was ist q?

Schüler: Das p ist die Zahl vor x. Das q ist die Zahl die alleine - also ohne irgend ein x - in der Gleichung steht.

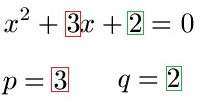
Oma: Verstehe ich dies richtig das p = 3 und q = 2 ist?

Schüler: Ja. Wir nehmen unser p und unser q und setzen dies in unsere Lösungsformel ein. Für p setzen wir 3 ein (rot markiert) und für q setzen wir 2 ein (grün markiert).

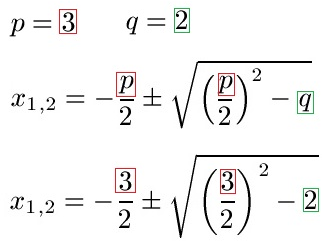
Wurzel und Bruch berechnen

Oma: Jetzt rechnen wir?

Schüler: Exakt. Wir haben vor der Wurzel einen Bruch stehen. Diesen rechnen wir aus und erhalten -1,5. Diese 3:2 steht auch noch einmal unter der Wurzel. Hier ergibt sich ebenfalls 1,5. Wir quadrieren dies, sprich wir berechnen 1,5 · 1,5 = 2,25. Die -2 bleibt stehen.

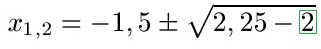
Oma: Jetzt die Wurzel ausrechnen?

Schüler: Ja. Wir rechnen aus: 2,25 - 2 = 0,25. Die Wurzel aus 0,25 ist 0,5. Wenn du es mir nicht glaubst benutze den Taschenrechner.

Oma: Ich glaube es dir ja. Was mache ich als nächstes?

Schüler: Ist dir das x_1,2 auf der linken Seite der Gleichung aufgefallen?

Oma: Jetzt wo du es sagst...

Schüler: Dies bedeutet, dass es zwei Lösungen geben sollte. Daher steht auf der rechten Seite auch ein plus und ein minus. Ob zuerst plus oder minus berechnet wird, spielt keine Rolle.

Oma: Heißt ich berechne -1,5 + 0,5 und ich berechne -1,5 - 0,5?

Schüler: Genau. Wir erhalten dadurch zwei Lösungen. Die eine Lösung ist x = -1 und die andere Lösung ist x = -2.

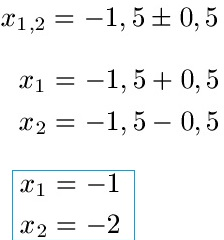
Oma: Aber hier steht doch x₁ und x₂?

Schüler: Das macht man einfach zum Durchnummerieren der Ergebnisse. Man kann x₁ und x₂ auch vertauschen.

Nullstellen berechnen

Oma: Jetzt habe ich zwei Lösungen für eine quadratische Funktion. Was soll das? Was bedeutet das?

Schüler: Die PQ-Formel liefert eigentlich die Nullstellen. Ich zeichne einfach mal irgend eine quadratische Funktion in ein Koordinatensystem. Die nächste Grafik hat nichts mit der Berechnung weiter oben zu tun. Sie ist nur ein Beispiel.

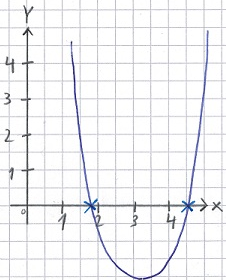
Oma: Da sind zwei kleine Kreuzchen gemacht. Was sollen die?

Schüler: Genau das sind die Nullstellen. Es sind die Punkte an denen y = 0 ist, sprich sie liegen genau auf der x-Achse. Genau diese Stellen rechnet man mit der PQ-Formel aus.

Oma: Das sind hier 2 Nullstellen. Ist dies immer so?

Schüler: Nein. Es kann auch passieren, dass es keine Nullstellen gibt oder eine doppelte Nullstelle.

Oma: Wann passiert das?

Schüler: Wir hatten doch vorhin eine Wurzel berechnet? Dazu muss die Zahl unter der Wurzel 0 oder größer sein. Aus einer negativen Zahl darf keine Wurzel gezogen werden. Es gibt dann keine Nullstellen, sprich y = 0 wird nie durch den Funktionsverlauf erreicht. Im Prinzip "funktioniert die PQ-Formel hier nicht".

Oma: Und was ist eine doppelte Nullstelle?

Schüler: Wenn unter der Wurzel 0 rauskommt. In diesem Fall sind x₁ und x₂ gleich groß. Dies nennt man dann doppelte Nullstelle.

Mitternachtsformel / ABC-Formel

Oma: Ich glaube das habe ich einigermaßen verstanden. Gibt es noch etwas, was man wissen sollte?

Schüler: Wenn vor x ein Bruch steht, zu Beispiel (4:3)x dann setzt man eben für p den Bruch 4/3 ein. Dies gilt auch bei negativen Zahlen. Haben wir -4x ist p = -4 und muss so in die Lösungsformel eingesetzt werden. Auch q kann negativ sein.

Oma: Gibt es eine einfache Alternative zur PQ-Formel?

Schüler: Naja, man kann den Taschenrechner verwenden *lach*.

Oma: Sollte ihr doch bestimmt nicht in der Schule.

Schüler: Stimmt. Also alternativ gibt es noch die Mitternachtsformel. Man nennt diese manchmal auch ABC-Formel.

Oma: Die ist besser?

Schüler: Das ist Geschmackssache. Man muss nicht für 1x² sorgen, sondern kann auch direkt rechnen wenn man 3x² hat.

Oma: Und jetzt?

Schüler: Auf die Herleitung der PQ-Formel habe ich gerade keine Lust. Wer die PQ-Formel lernen möchte, sollte vielleicht noch einige Aufgaben selbst lösen.

Oma: Übung macht den Meister.

Schüler: Stimmt. Ist manchmal lästig. Aber so ist es eben.

PQ-Formel Aufgaben / Übungen

Aufgabe 1: Glaubt ihr das Thema PQ-Formel verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Da viele Schüler jedoch schon bei den Begriffen scheitern, fangen wir mit einfachen Fragen dazu an. Fragen und Aufgaben können per Klick übersprungen werden.

• Was berechnet man mit der PQ-Formel eigentlich?

• Winkel
• Nullstellen
• Strahlensatz
• Hypotenuse

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 7 Aufgaben erfolgreich gelöst.