Brüche multiplizieren und dividieren

Wie funktioniert das Multiplizieren oder Dividieren von Brüchen? Wie wird aus der Division eines Bruchs eine Multiplikation? Und wie werden drei Brüche dividiert? Ich versuche die Inhalte so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde. Die Inhalte liegen als Text und als Video vor.

Brüche zu multiplizieren und zu dividieren gehört zu den Grundlagen der Bruchrechnung. Eine kurze Erinnerung: Das Rechnen mit Brüchen bedeutet mit Anteilen an etwas Ganzem zu rechnen. So können zum Beispiel mit einer Multiplikation 3 von 8 Teile verdoppelt werden auf 6 von 8 Teilen

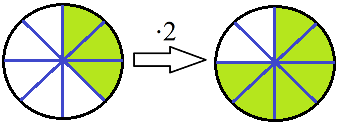
Oder umgekehrt: 6 von 8 Teile können halbiert werden auf 3 von 8 Teile.

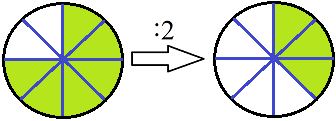
Wie die Multiplikation oder Division von Brüchen funktioniert, sehen wir uns in den nächsten Abschnitten an.

Wie werden Brüche multipliziert oder dividiert?

Um Brüche zu multiplizieren wird Zähler mit Zähler und Nenner mit Nenner multipliziert. Im nächsten Beispiel ergibt sich im Zähler 3 · 5 = 15 und im Nenner 2 · 4 = 8.

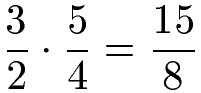
Die Multiplikation von Brüchen lässt sich allgemein mit einer Gleichung (und Variablen) darstellen.

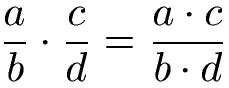
Um Brüche zu dividieren wird die Division in eine Multiplikation umgewandelt. Dies bedeutet das Geteiltzeichen (:) durch ein Malzeichen (·) zu ersetzen. Um dies tun zu dürfen, wird beim zweiten Bruch Zähler und Nenner vertauscht. Dadurch entsteht die Multiplikation zweier Brüche. Diese wird gelöst durch Multiplikation von Zähler mal Zähler und Nenner mal Nenner.

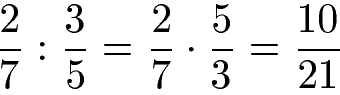
Das Vertauschen von Zähler und Nenner wird auch Kehrwert bilden genannt. Die Division von Brüchen lässt sich auch allgemein schreiben mit der folgenden Gleichung.

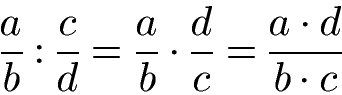
Anzeigen:

Wie werden Brüche nach der Multiplikation oder Division gekürzt?

In vielen Fällen können Brüche nach der Multiplikation oder Division durch Kürzen vereinfacht werden. Kürzen bedeutet den Zähler und den Nenner eines Bruchs durch die gleiche Zahl zu teilen. Dabei entsteht ein Bruch mit kleineren Zahlen.

Als Beispiel dient die Multiplikation zweier Brüche. Zähler wird mit Zähler multipliziert und Nenner mit Nenner. Als Produkt entsteht der Bruch 12 : 40. Dieser kann durch Kürzen vereinfacht werden. Dazu werden Zähler und Nenner durch 4 geteilt.

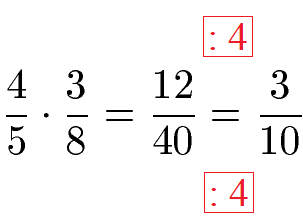
Im nächsten Beispiel werden zwei Brüche dividiert. Dazu wird das Geteiltzeichen durch ein Malzeichen ausgetauscht. Beim zweiten Bruch werden Zähler und Nenner vertauscht. Als Lösung entsteht der Bruch 6 : 32. Dieser wird mit 2 gekürzt.

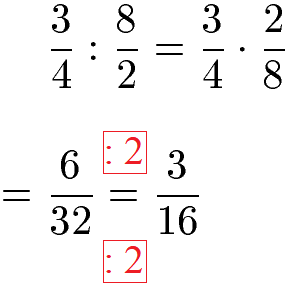
Wie kann man 3 Brüche dividieren?

Um 3 Brüche zu dividieren wird Schrittweise von links nach rechts gerechnet. Als Beispiel soll die Division der folgenden drei Brüche dienen.

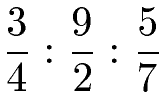
Zunächst steht die Division der beiden linken Brüche an. Durch Multiplikation mit dem Kehrwert wird die Berechnung durchgeführt. Dies bedeutet das Geteiltzeichen durch ein Malzeichen zu ersetzen und beim zweiten Bruch Zähler und Nenner zu vertauschen.

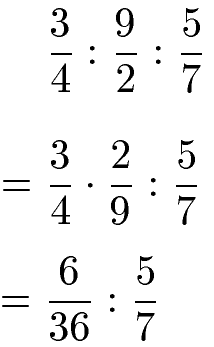
Aus der Division von drei Brüchen wurde eine Division aus zwei Brüchen. Diese können ganz normal wie die Division von Brüchen berechnet werden: Multiplikation mit dem Kehrwert.

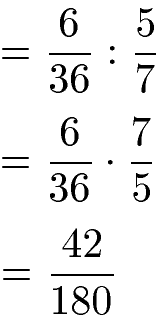
Das Ergebnis 42 : 180 kann noch vereinfacht werden. Zunächst kann der Bruch mit 2 gekürzt werden, sprich Zähler und Nenner werden durch 2 geteilt. Um den Bruch jedoch vollständig zu kürzen wird im Anschluss noch einmal durch 3 in Zähler und Nenner geteilt.

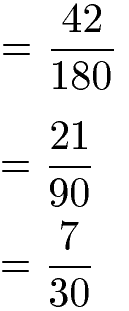
Hinweis: Der Bruch 42 : 180 kann selbstverständlich auch gleich mit 6 gekürzt werden. Das Schrittweise kürzen erst mit 2 und danach mit 3 dürfte für viele Menschen jedoch einfacher sein.