Prozentrechnung Erklärung und Beispiel

Kann man die Prozentrechnung so einfach erklären, dass jeder diese versteht? Wir versuchen es hier. Stellt euch vor ein Schüler kommt nach der Schule zu seiner Oma und versucht ihr zu erklären, wie das Rechnen mit Prozenten funktioniert. Glaubt ihr eine echte Oma würde die folgenden Erklärungen verstehen?

Schüler: Morgen soll es beim Einkaufen 20 Prozent Rabatt geben. Weiß du was das heißt?

Oma: Das es billiger wird?

Schüler: Ja. Wir haben vor kurzem in der Schule gelernt, wie das Rechnen mit Prozenten funktioniert. Weißt du noch wie das geht?

Oma: Nein. Keine Ahnung. So grob weiß ich was rauskommen müsste, aber wirklich rechnen kann ich das nicht mehr.

Schüler: Starten wir damit was ein Prozent überhaupt ist. Ein Prozent ist nichts anderes als 1 durch 100. Man kürzt dabei Prozent mit % ab. Dies bedeutet auch, dass 21 % nichts anderes ist als 21 : 100.

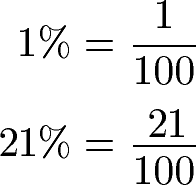
Oma: Wenn es heißt, dass 50 % der Personen in einem Raum Männer sind, dann bedeutet dies das 50 von 100 Menschen in dem Raum männlich sind?

Schüler: Das wäre eine Möglichkeit. Aber es könnten auch 100 von 200 Menschen männlich sein oder 5 von 10 Menschen. In der Prozentrechnung gibt man im Prinzip einen rechnerischen Anteil an 100 an.

Formel und Beispiel Prozentwert

Schüler: Nehmen wir noch einmal das Rabatt-Beispiel. Sagen wir etwas zu Essen kostet 1,69 Euro. Ab morgen gibt es darauf 20 Prozent Rabatt. Wie viel billiger wird es?

Oma: Naja das sind ein paar Cent die es weniger kostet.

Schüler: Stimmt. Ich glaube wir brauchen jetzt einmal die Formel für die Prozentrechnung. Wir möchten einen Anteil ausrechnen, diesen nennt man Prozentwert W. Wir wissen wie viel Rabatt es gibt, also den Prozentsatz, den es billiger wird. Den kürzt man mit p % ab. Und wir wissen was es ursprünglich kostet, also den Grundwert G.

Oma: Verstehe ich noch nicht ganz. Rechne mal vor.

Schüler: Wir nehmen die folgende Formel und setzen 20 % ein - denn so groß ist der Rabatt - und wir setzen den Grundwert G mit 1,69 Euro ein. Danach müssen wir nur noch rechnen. Aus den 20 % machen wir 20 : 100. Danach können wir - egal ob mit oder ohne Taschenrechner - einfach den Rabatt von 0,34 Euro ausrechnen.

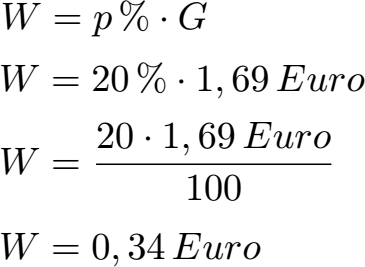
Oma: Da steht aber nicht Rabatt sondern W.

Schüler: Das W ist der Prozentwert, also der Anteil am Ganzen, den wir berechnen wollten.

Oma: OK. Das heißt wir müssen nicht mehr 1,69 Euro bezahlen, sondern wir bekommen 0,34 Euro Rabatt darauf.

Schüler: So ist es. Statt 1,69 Euro müssen wir nur noch 1,35 Euro bezahlen.

Anzeigen:

Formel und Beispiel Prozentsatz

Schüler: Machen wir einmal weiter mit der Einführung in die Prozentrechnung.

Oma: Bitte weiterhin eine Erklärung für Dumme.

Schüler: Angenommen wir wüssten nicht, dass es 20 % günstiger geworden ist. Wir wüssten stattdessen, das es 0,34 Euro billiger geworden ist und es vorher 1,69 Euro gekostet hat. Weiß du jetzt wie man auf die 20 % Rabatt kommt?

Oma: Keine Ahnung. Dafür gibt es sicher auch eine Formel?

Schüler: Eigentlich müssen wir die Formel der Prozentrechnung nur nach dem Prozentsatz umstellen und rechnen. Heißt wir brauchen die Formel nach p % umgestellt. Auch hier ist der Anteil am Ganzen wieder der Prozentwert W mit 0,34 Euro und insgesamt haben wir den Grundwert G mit 1,69 Euro. Wir setzen dies ein und rechnen.

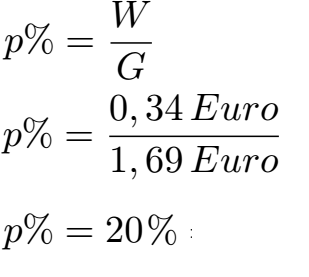
Oma: Da sind wieder die 20 Prozent Rabatt. Und wenn ich den Preis vor und nachher habe?

Schüler: Dann haben wir wieder den Grundwert G mit 1,69 Euro. Der neue Preis nach dem Rabatt war 1,35 Euro. Dies ist unser Anteil am Ganzen, dem Prozentwert W.

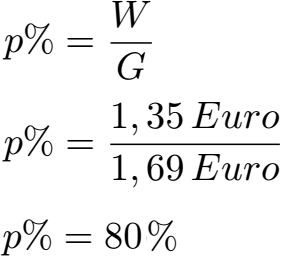
Oma: Da kommen jetzt aber 80 Prozent raus?

Schüler: Klar. Der Preis ist von 100 Prozent auf 80 Prozent gefallen.

Formel und Beispiel Grundwert

Schüler: Wir haben noch eine dritte Möglichkeit vergessen.

Oma: Wir wissen nicht was das Essen vor dem Rabatt gekostet hat.

Schüler: Genau. Der reduzierte Preis liegt bei 1,35 Euro und der Rabatt lag bei 20 Prozent. Was hat das Essen ursprünglich gekostet?

Oma: Wieder irgend eine Formel zur Prozentrechnung?

Schüler: Ja, dieses Mal nach G umgestellt. Wir setzen den Anteil am Ganzen mit W = 1,35 Euro ein. Dieser Preis sind 80 Prozent vom Grundwert (20 Prozent Rabatt).

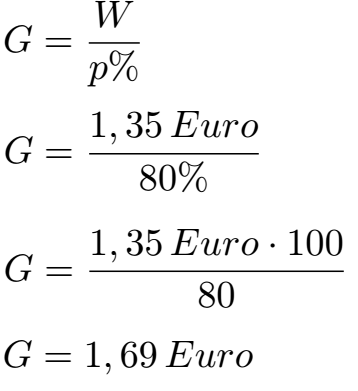
Oma: Damit ich das richtig verstehe: Die 1,35 Euro sind 80 Prozent des Preises. Und die 1,69 Euro sind 100 Prozent des Preises, also der ursprüngliche Preis?

Schüler: So ist es.

Prozentrechnung anwenden

Oma: Die Beispiele habe ich denke ich verstanden. Wofür braucht man die Prozentrechnung denn noch?

Schüler: Die Zinsrechnung ist denke ich die wichtigste Anwendung der Prozentrechnung. Es geht dabei zum Beispiel darum Zinsen auf Geldanlagen zu berechnen. Die nächste Anwendung ist der Dreisatz. Das zu erklären ist jedoch ein eigenes Thema. Das machen wir ein anderes Mal.

Oma: OK. Also merke ich mir, dass man die Prozentrechnung im echten Leben wirklich gebrauchen kann.

Schüler: Ja, manchmal macht man im Mathematik-Unterricht sogar etwas für die Realität.

Oma: Ich vermute solche Dinge werden auch beim Einstellungstest nachgefragt?

Schüler: Das meinte der Lehrer auch einmal. Aber da habe ich noch ein bisschen Zeit bis ich dort sitze.

Oma: Was machen eigentlich Schüler beim Prozentrechnen falsch?

Schüler: Ich glaube vielen ist gar nicht klar, dass 1 Prozent nichts anderes als ein Hundertstel ist. Oder sie können ohne Taschenrechner nicht mal grob überlegen, was denn als Ergebnis rauskommt. Manchmal bekommt man beim Rechnen etwas ganz falsches raus und wenn man das Thema nicht versteht und nicht überschlagen kann, sieht man gar nicht, dass der Taschenrechner Mist liefert.

Oma: Verstehe ich. Wie lerne ich das Thema?

Schüler: Üben, üben und nochmals üben.

Oma: Dann mach mal.

Aufgaben / Übungen Prozentrechnung

Aufgabe 1:

Glaubt ihr das Thema Prozentrechnung verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Da viele Schüler jedoch schon bei den Begriffen scheitern, fangen wir mit einfachen Fragen dazu an. Fragen und Aufgaben können per Klick übersprungen werden.

• 1 % ist nichts anderes als ein...

• ... Millionstel
• ... Hundertstel
• ... Zehntel
• ... Tausendstel

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 7 Aufgaben erfolgreich gelöst.