Bruchrechnen einfach erklärt

Die Bruchrechnung lernst du in diesem Artikel mit Text und Video. Du erfährst wozu ein Bruch gut ist und wie mit Brüchen gerechnet wird. Dazu sehen wir uns an wie das Erweitern und Kürzen von Brüchen funktioniert sowie alle Grundrechenarten (Addition, Subtraktion, Multiplikation und Division). Ich versuche die Inhalte so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde.

Ein Bruch dient dazu einen Anteil von etwas Ganzen darzustellen, zum Beispiel einen Teil von einem Kuchen oder einen bestimmten Anteil einer Gruppe von Personen. Sehr schön zu verstehen ist dies mit einer Pizza: Die nächste Pizza wurde in 8 gleich große Teile zerschnitten. Die Anzahl aller Teile werden wir später als Nenner bezeichnen.

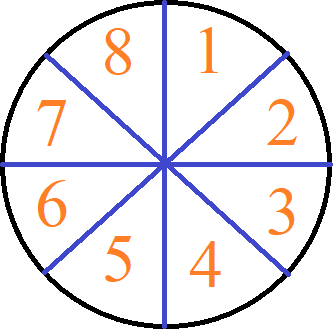
Von der Pizza werden 3 Stück gegessen, genauer gesagt 3 von 8 Stücke. Es bleiben 5 von 8 Stücke übrig. Die nächste Grafik zeigt dies in grün und rot.

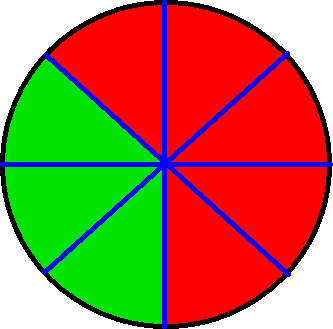
Die beiden Brüche für gegessen und nicht gegessen wären damit diese:

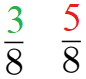
Bruchrechnung: Wie werden Brüche gekürzt?

Brüche zu kürzen bedeutet den Zähler und den Nenner des Bruchs durch die gleiche Zahl zu teilen. Der Wert des Bruchs ändert sich durch das Kürzen nicht. Die nächste Grafik zeigt wie ein Bruch mit 5 von 10 Teile auf 1 von 2 Teile gekürzt wird. Die gebe Fläche bleibt dabei jedoch gleich groß.

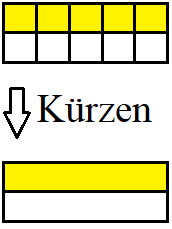
Das Kürzen von Brüchen dient dazu Brüche zu vereinfachen. In vielen Fällen kann ein Bruch mit 2 oder 3 gekürzt werden. Dazu wird der Zähler und der Nenner durch die gleiche Zahl geteilt. Im nächsten Beispiel wird der Bruch mit 2 gekürzt.

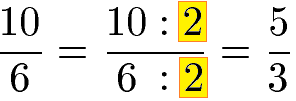
Im nächsten Beispiel würde ein Kürzen des Bruchs mit 2 zu Dezimalzahlen (= Kommazahlen) führen. Jedoch können sowohl die 15 als auch die 12 ohne Rest durch 3 geteilt werden. Daher wird der Bruch mit 3 gekürt.

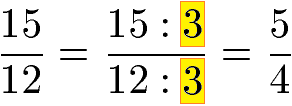
Zähler und Nenner werden beim Kürzen durch die gleiche Zahl geteilt. Es ist daher wichtig einen passenden Teiler für beide Zahlen zu finden. Wie du diesen findest lernst du mit den Teilbarkeitsregeln. Weitere Beispiele findest du außerdem unter Brüche kürzen.

Anzeigen:

Bruchrechnung: Wie kann man einen Bruch erweitern?

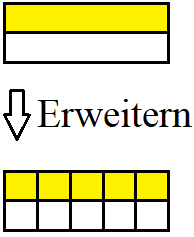
Brüche zu erweitern bedeutet den Zähler und den Nenner des Bruchs mit der gleichen Zahl zu multiplizieren. Das Erweitern des Bruches wird dabei mit einer natürlichen Zahl (1, 2, 3, 4 und so weiter) durchgeführt. Auch beim Erweitern eines Bruches ändert sich dessen Wert nicht. In der nächsten Grafik wird die gelbe Fläche mit 1 von 2 Teilen auf 5 von 10 Teilen erweitert. Die gelbe Fläche bleibt dabei jedoch gleich groß.

Der nächste Bruch mit 3 durch 4 wird mit der Zahl 2 erweitert. Das Erweitern eines Bruchs mit 2 bedeutet den Zähler und den Nenner mit 2 zu multiplizieren.

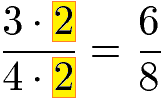
Im Prinzip kann mit jeder natürlichen Zahl erweitert werden. In der nächsten Aufgabe wird mit 3 erweitert, sprich Zähler und Nenner werden mit 3 multipliziert.

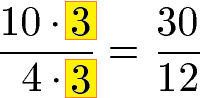
Das Erweitern von Brüchen dient dazu Brüche im Anschluss addieren oder subtrahieren zu können. Dies sehen wir uns als nächstes an.

Bruchrechnen: Wie addiert oder subtrahiert man Brüche?

Um Brüche zu addieren oder zu subtrahieren werden zunächst die Brüche auf den gleichen Nenner gebracht. Im Anschluss werden die Zähler addiert oder subtrahiert während der Nenner einfach in das Ergebnis übernommen wird.

Im einfachsten Fall sind die Nenner der Brüche bereits gleich. Dies wird in der Mathematik als gleichnamige Brüche bezeichnet. Sind die Brüche gleichnamig können die Zähler einfach addiert werden und der Nenner wird beibehalten.

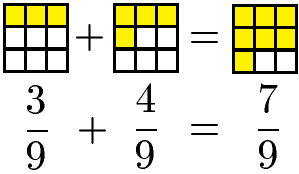
Die Subtraktion gleichnamiger Brüche ist ebenfalls sehr einfach. Die Zähler werden subtrahiert und der Nenner wird beibehalten.

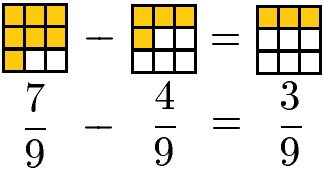
Ungleichnamige Brüche:

Sind die Nenner verschieden (= ungleichnamige Brüche) müssen diese für die Addition oder Subtraktion der Brüche zunächst gleichnamig gemacht werden. Als Beispiel dient eine Aufgabe mit 4 und 3 als Nenner.

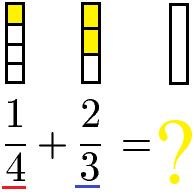
Um die Brüche gleichnamig zu machen wird zunächst ein neuer Nenner benötigt. Diesen erhalten wir durch Multiplikation der beiden Ausgangsnenner:

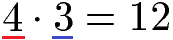
Im nächsten Schritt müssen wir beide Brüche erweitern. Zur Erinnerung: Erweitern bedeutet den Zähler und den Nenner eines Bruchs mit der gleichen Zahl zu multiplizieren. Wir müssen dabei so erweitern, dass wir auf 12 im Nenner kommen. Für den ersten Bruch bedeutet dies mit 3 zu erweitern, den zweiten Bruch erweitern wir mit 4. Dadurch erhalten wir zwei Brüche mit 12 im Nenner, die wir einfach addieren können.

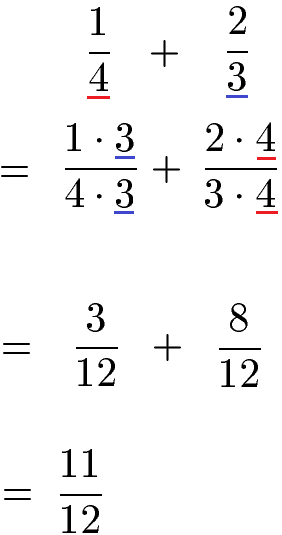
Weitere Beispiele findest du unter Brüche addieren und subtrahieren.

Bruchrechnen: Wie berechne ich Brüche mal und geteilt?

Brüche mal zu rechnen bedeutet die Zähler miteinander zu multiplizieren und die Nenner miteinander zu multiplizieren: Zähler mal Zähler und Nenner mal Nenner. Mehr gibt es zur Multiplikation von Brüchen erst einmal nicht zu verstehen. Ein Beispiel:

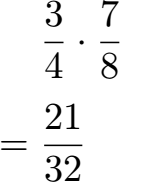
Brüche geteilt zu rechnen bedeutet die Geteiltaufgabe in eine Malaufgabe umzuwandeln. Dazu wird das Geteiltzeichen (:) durch ein Malzeichen (·) ersetzt. Um dies zu tun dürfen wird beim zweiten Bruch Zähler und Nenner vertauscht. Die Malaufgabe lösen wir erneut mit Zähler mal Zähler und Nenner mal Nenner.

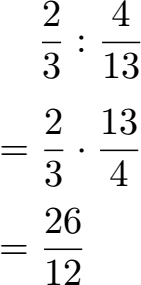
Weitere Beispiele findest du unter Brüche multiplizieren und dividieren.

Welche Regeln gibt es beim Bruchrechnen?

Zur Bruchrechnung solltest du dir einige wichtige Regeln merken und eine Reihe an Dingen auswendig wissen.

Regeln der Bruchrechnung:

1. Die Zahl über dem Bruchstrich nennt man Zähler.
2. Die Zahl unter dem Bruchstrich nennt man Nenner.
3. Für die Addition von Brüchen muss der Nenner erst gleich gemacht werden.
4. Für die Subtraktion von Brüchen muss der Nenner erst gleich gemacht werden.
5. Bei der Multiplikation wird Zähler mal Zähler und Nenner mal Nenner gerechnet.
6. Aus einer Division wird eine Multiplikation durch Vertauschen von Zähler und Nenner beim zweiten Bruch.

Aufgaben / Übungen Bruchrechnen

Aufgabe 1:

Glaubt ihr das Thema Bruchrechnung verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Da viele Schüler jedoch schon bei Basiswissen scheitern, fangen wir mit einfachen Fragen dazu an. Fragen und Aufgaben können per Klick übersprungen werden.

• Wie nennt man die Zahl, welche bei einem Bruch oben steht?

• Bruchstrich
• Eulersche Zahl
• Zähler
• Nenner

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 7 Aufgaben erfolgreich gelöst.