Mitternachtsformel / ABC-Formel
Geschrieben von: Dennis RudolphDienstag, 07. Juli 2020 um 17:41 Uhr
Kann man die Mitternachtsformel / ABC-Formel so einfach erklären, dass jeder diese versteht? Wir versuchen es hier. Stellt euch vor ein Schüler kommt nach der Schule zu seiner Oma und versucht ihr zu erklären, was diese Formel ist und wie man sie benutzt. Glaubt ihr eine echte Oma würde die folgenden Erklärungen verstehen?
Schüler: Hast du schon einmal etwas von der Mitternachtsformel oder ABC-Formel gehört?
Oma: Nein.
Schüler: Diese benutzt man um quadratische Gleichungen oder quadratische Funktionen zu lösen.
Oma: Ich verstehe kein Wort. Das musst du mir erklären.
Schüler: Wir hatten einmal das Gleichungen umformen besprochen. Dabei versucht man eine Gleichung so zu verändern, dass man x berechnet. Es kann jedoch passieren, dass es nicht x in einer Gleichung gibt, sondern x2, sprich die Abkürzung für x · x.
Oma: Ich löse eine Gleichung mit x2 dadurch das ich die Mitternachtsformel verwende?
Schüler: Genau. Ganz wichtig ist, dass es kein x3, x4 oder höher gibt. Zum Beispiel diese quadratische Gleichung könnte man mit der Mitternachtsformel lösen:
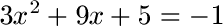
Sobald du diesen Artikel verstanden hast, stelle dir mal folgende Frage: Kannst du Aufgaben zur ABC-Formel selbst lösen? Finde es raus mit unseren Fragen und Aufgaben zu diesem Thema. Weiter zur ersten Aufgabe Mitternachtsformel.
ABC-Formel Beispiel
Oma: Ist ABC-Formel und Mitternachtsformel das selbe?
Schüler: Ja. Ich mache mal ein Beispiel. Nehmen wir die Gleichung von eben:
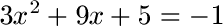
Oma: Wie fange ich an?
Schüler: Zunächst müssen wir die Gleichung so verändern, dass wir = 0 erhalten. Aus diesem Grund müssen wir die -1 beseitigen. Dazu rechnen wir auf beiden Seiten der Gleichung +1. Auf der linken Seite wird aus der 5 eine 6. Auf der rechten Seite entsteht eine 0.
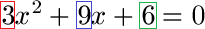
Oma: Wieso hast du die 3, 9 und 6 farbig markiert?
Schüler: Die brauchen wir jetzt. Wir lesen jetzt a, b und c ab.
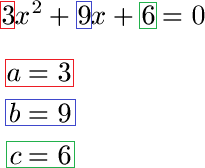
Oma: OK. Daher auch der Name ABC-Formel. Was mache ich damit jetzt?
Anzeigen:
Formel der Mitternachtsformel
Schüler: Wir brauchen als nächstes die Formel um solche quadratischen Gleichungen lösen zu können.
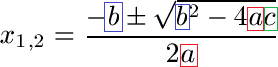
Oma: Sieht sehr verwirrend aus. Was soll ich damit?
Schüler: Wir setzen hier für a, b und c die entsprechenden Zahlen ein, die wir oben abgelesen haben.
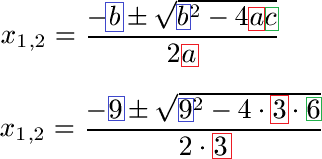
Oma: Sieht schon einfacher aus. Im Anschluss rechne ich?
Schüler: Ja. Wir rechnen alles unter der Wurzel aus und im Nenner machen wir aus 2 · 3 = 6. Dadurch wirkt alles auch gleich viel aufgeräumter.
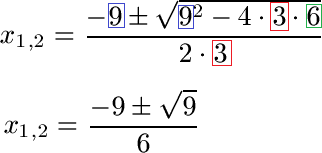
ABC-Formel Lösung berechnen
Oma: Ich sehe da dieses plus und minus übereinander. Was soll das?
Schüler: Dazu kommen wir gleich. Ich ziehen erst einmal die Wurzel aus 9. Das Ergebnis ist 3. Das plus-minus bedeutet, dass wir zwei Lösungen haben. Wir berechnen den Bruch einmal mit einem plus und einmal mit einem minus. Dadurch erhalten wir zwei Lösungen für unsere quadratische Gleichung.
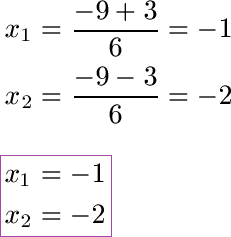
Oma: Was soll das mit x1 und x2?
Schüler: Man nummeriert die Ergebnisse durch. Dabei ist x1 die erste Lösung und x2 die zweite Lösung der Gleichung. Allerdings ist es unwichtig, ob wir x1 = -1 oder x1 = -2 haben bzw. x2 = -2 oder x2 = -1. Wichtig ist nur, dass wir beide Nullstellen berechnen.
Oma: Was sind denn Nullstellen?
Nullstellen und PQ-Formel
Schüler: Wir haben am Anfang die Angaben = 0 gesetzt. Damit haben wir im Prinzip gesagt, dass wir die Punkte suchen, bei denen y = 0 ist. Ich zeichne einmal eine Funktion in ein Koordinatensystem. Wichtig: Das ist nicht die Gleichung von weiter oben, sondern irgend eine quadratische Funktion.
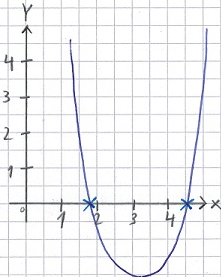
Schüler: Die Stellen bei denen y = 0 beim Funktionsverlauf ist habe ich mit einem kleinen Kreuzchen markiert. Es sind damit die Punkte, an denen der Funktionsverlauf die x-Achse schneidet.
Oma: Verstehe ich... so in etwa. Muss ich noch etwas wissen?
Schüler: Wenn beim Rechnen mit der ABC-Formel unter der Wurzel eine 0 auftaucht ist das plus-Ergebnis und das minus-Ergebnis gleich. Die Nullstellen liegen beide an einer Stelle. Das nennt man doppelte Nullstelle. Ist die Zahl unter der Wurzel negativ wird die Rechnung abgebrochen. Es gibt dann keine Nullstellen, also erreicht der Graph der Funktion nie die x-Achse.
Oma: Und was ist wenn ich die Mitternachtsformel nicht mag?
Schüler: Dann kannst du quadratische Funktionen auch mit der PQ-Formel lösen.
Aufgaben / Übungen Mitternachtsformel
Meistgelesene Inhalte
- Allgemenbildung Quiz
- Prozentrechnung
- Bruchrechnen
- Satz des Pythagoras
- PQ-Formel
- Mitternachtsformel
- Polynomdivision
- Zinsrechnung
- Gleichungen umformen
- Nullstellen bestimmen
- Dreisatz
Neue Artikel
- Rationale Zahlen ▷ Ist eine Zahl rational?
- Bruch in Kommazahl (Dezimalzahl) umwandeln
- Koordinatensystem: Erklärung und Punkte
- Brüche kürzen und erweitern
- Brüche multiplizieren und dividieren
- Rechteck Eigenschaften: Flächeninhalt, Umfang und mehr
- Brüche addieren und subtrahieren
- Sachaufgaben Klasse 5 Mathematik
- Flächeninhalt Rechteck ▯ Beispiele + Erklärung
- Umfang Rechteck mit Formeln berechnen
